Dezimalzahlen 5.Klasse kostenlose Aufgabenblätter
Kostenlose Arbeitsblätter zum Download als PDF, zum Thema Dezimalzahlen in der 5. Klasse. Viele Beispiele zum Üben zu den Grundrechenarten mit Dezimalzahlen.
Grundlagen
Dezimalzahlen beziehungsweise Kommazahlen erkennt man an dem Komma. Sie bestehen aus den Vorkommastellen, dem Komma und den Nachkommastellen.
Arten von Dezimalzahlen
Man kann sie in drei Kategorien einteilen:
- endliche/abbrechende Dezimalzahlen
- periodische Dezimalzahlen
- irrationale Zahlen.
Endliche Dezimalzahlen haben eine endliche Zahl an Nachkommastellen, also gehen nicht bis ins unendliche weiter. Bei periodischen Dezimalzahlen wiederholt sich eine Ziffer oder Ziffernkombination der Nachkommastellen bis ins unendliche. Die irrationalen Zahlen haben auch unendlich viele Nachkommastellen, sind aber trotzdem nicht periodisch. Ein Beispiel für eine irrationale Zahl, welches weit verbreitet ist, ist die Zahl Pi.
Stellenwerttabelle
Wir können auch Dezimalzahlen in Stellen einteilen. Bisher kennen wir ja nur die Namen der Vorkommastellen, also Einer, Zehner, Hunderter, und so weiter. Nachkommastellen heißen so ähnlich, wir sprechen aber von Zehnteln(z), Hundertsteln(h), Tausendsteln(t), Zehntausendsteln(zt), Hunderttausendsteln(ht), und so weiter.
Hier kannst du eine Stellenwerttabelle sehen:
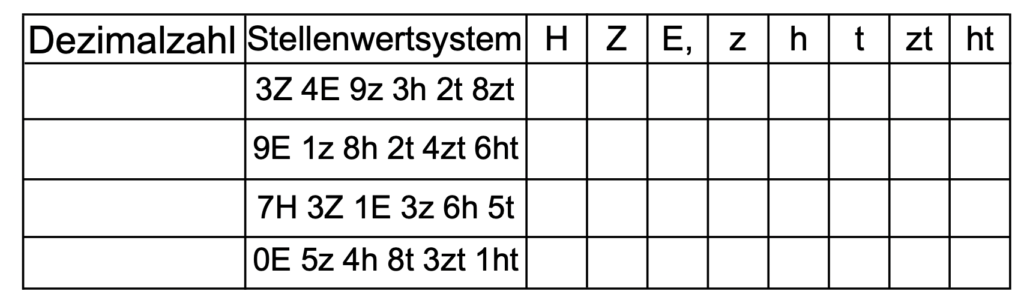
Runden von Dezimalzahlen
Wichtig ist auch, dass Dezimalzahlen oft gerundet werden, denn manchmal macht es keinen Sinn Ergebnisse extrem genau anzugeben. Ein Beispiel wären Geldbeträge. Hier wären mehr als zwei Nachkommastellen sinnlos, denn diese geben die Cent Beträge an und kleinere Geldformen als Cent haben wir nicht.
Beim Runden von Zahlen geht es darum auf die nächstgrößere/-kleinere Zahl auf-/abzurunden. Zuerst entscheiden wir auf welche Stelle wir runden möchten. Beispielsweise haben wir die Zahl 563,53. Wir entscheiden uns, dass wir auf zehntel runden möchten. Wir markieren für das Verständnis die zehntel-Stelle rot.
Als nächstes müssen wir die Ziffer rechts von der besagten Stelle betrachten, wir markieren diese Ziffer orange. Nun überprüfen wir, ob diese kleiner als 5, also {0, 1, 2, 3, 4}, oder größer gleich 5 ist, also {5, 6, 7, 8, 9}. Ist sie kleiner runden wir ab, ansonsten runden wir auf. Abrunden bedeutet die Stelle, auf welche wir runden, bei uns die zehntel-Stelle, bleibt gleich und alles rechts davon wird 0. Aufrunden bedeutet die Stelle, auf welche wir runden, wird um 1 erhöht und alles rechts davon wird 0. In unserem Fall runden wir ab, denn 3 < 5.
Die auf die zehntel Stelle gerundete Zahl ist also 563,5.
Grundrechenarten
Kommen wir zu den Grundrechenarten. Hier gibt es keinen großen Unterschied zu den natürlichen Zahlen. Wichtig ist nur das Komma immer an der richtigen Stelle zu behalten.
Falls ihr vorher erstmal grundsätzlich die Grundrechenarten wiederholen möchtet, könnt ihr das hier tun!
Dezimalzahlen addieren & subtrahieren
Fangen wir mit Addieren an:
Falls die Zahlen unterschiedlich viele Nachkommastellen haben, füllen wir mit Nullen auf, dies hilft für das Verständnis, verändert die Zahl nicht aber nicht:
z.B. 491,11 + 203,5612
Beim Subtrahieren läuft es genau gleich ab. Kommen wir also gleich zum Multiplizieren.
Dezimalzahlen multiplizieren
Hier ignorieren wir das Komma/die Kommas während des Rechnens und fügen es am Ende wieder hinzu.
Nun müssen wir das Komma wieder hinzufügen. Dafür zählen wir die Anzahl der Nachkommastellen aller Zahlen aus der Angabe. 43,15 hat zwei und 23,2 hat eine. Also sind es insgesamt 3 Nachkommastellen. Wir setzen das Komma beim Ergebnis so, dass wir auch wieder drei Nachkommastellen haben.
Dezimalzahlen dividieren
Als nächstes kommen wir zum Dividieren. Hier musst du die Kommastelle des Divisors, als der zweiten Zahl, so lange verschieben, bis sie keine Nachkommastelle hat, aber Achtung: das Komma der ersten Zahl, als vom Dividenden, muss um gleich viele Stellen verschoben werden. Angenommen wir wollen 13,54 : 0,2 rechnen. Wir müssen das Komma bei 0,2 um eins nach links verschieben um keine Nachkommastellen mehr zu haben, also 2. Dadurch müssen wir aber auch bei 13,54 das Komma um eins nach links verschieben, also 135,4. Nun können wir ganz normal schriftlich dividieren!
Bevor wir die 4 nach unten holen können müssen wir das Komma, welches vor der 4 steht, notieren! Anschließend können wir ganz normal fertig dividieren.
Falls ihr euch noch unsicher seid, könnt ihr einfach bei unserem YouTube Kanal vorbeischauen!
