Brüche 6. Klasse Kostenlose Aufgabenblätter
Kostenlose Arbeitsblätter für Schüler zum Thema Brüche und wie man diese addiert, subtrahiert, multipliziert, dividiert, kürzt & erweitert. Zu jedem Beispiel gibt es ein Erklärvideo wo die Lösung genau besprochen wird.
Grundlagen
Brüche sind immer ein Anteil von Etwas, in Zahlen dargestellt. Hier zum Beispiel haben die zwei violett markierten Pizzastücke einen Anteil von 2/8, da es insgesamt acht Pizzastücke gibt. Brüche kommen somit auch im echten Leben vor und sind wirklich nützlich. Wenn du lieber mit Videos lernst gib in Youtube Mathemuffel ein und unser Kanal sollte ganz oben erscheinen. Wir haben eine Playlist „Brüche“ angelegt wo du alle Videos zum Thema finden kannst.

Es gibt drei verschiedene Arten von Brüchen:
1. echter Bruch: Der Zähler ist kleiner als der Nenner
2. unechter Bruch: Der Zähler ist größer als der Nenner
3. gemischter Bruch: eine ganze Zahl + ein Bruch
Ein Bruch hat immer drei Bestandteile:
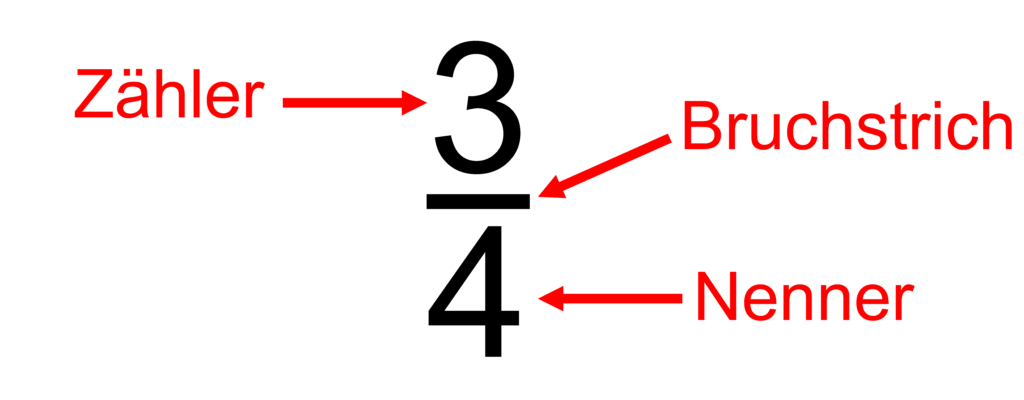
Brüche kürzen & erweitern
Brüche zu kürzen und zu erweitern ist ein wichtiger Grundstein im Rechnen mit Brüchen. Bei dem Kürzen von Brüchen dividieren wir Zähler und Nenner des Bruches durch die gleiche Zahl. In diesem Beispiel teilen wir durch 2. Dieses Vorgehen hilft uns Brüche einfacher darzustellen. Beim Erweitern von Brüchen machen wir genau das Gegenteil, wir multiplizieren Zähler und Nenner mit der gleichen Zahl. Das ist essenziell wenn man Brüche addieren oder subtrahieren will. Die Schwierigkeit liegt hierbei darin die passende Zahl für das Multiplizieren zu finden. In dem Beispiel erweitern wir den Bruch 1/4 mit 2.

Brüche addieren
Um Brüche zu addieren müssen wir im ersten Schritt die Bruchzahlen auf den selben Nenner bringen. Hierfür überlegen wir uns das kleinste gemeinsame Vielfache. Das kgV ist die kleinste gemeinsame Zahl die sich in beiden Malreihen der Nenner findet. In diesem Fall wäre es 6. Anschließend erweitern wir die Brüche so, dass beide auf das kleinste gemeinsame Vielfache kommen. Zuletzt muss man nur noch Zähler mit Zähler addieren und schon ist es geschafft

Brüche subtrahieren
Auch beim Subtrahieren von Brüchen dreht es sich darum das kleinste gemeinsame Vielfache zu finden. Wenn wir beide Bruchzahlen auf den selben Nenner gebracht haben, müssen wir die Differenz der beiden Zähler errechnen und der Nenner bleibt unverändert. In diesem Fall ist das kgV 8 und wir erweitern beide Brüche, sodass wir mit beiden Nennern auf 8 kommen. Dann müssen wir nur noch 2 von 6 abziehen und schon haben wir das Ergebnis.

Brüche multiplizieren
Um einen Bruch zu multiplizieren müssen wir ganz einfach nur den ersten Zähler mit dem zweiten Zähler multiplizieren und den ersten Nenner mit dem zweiten Nenner multiplizieren. In diesem Beispiel rechnen wir also zuerst 7*1=7 und 8*2=16 und können dann als Ergebnis 7/16 aufschreiben.

Brüche dividieren
Damit wir Bruchzahlen dividieren können müssen wir zuerst den Kehrwert des zweiten Bruches berechnen. Klingt kompliziert, ist es aber nicht. Im Prinzip müssen wir hierfür nur Zähler und Nenner vertauschen. Dies ist dann der Kehrwert. Mit dem Kehrwert wird nun multipliziert anstatt dividiert. Wir umgehen quasi das Dividieren. In unserem Beispiel brauchen wir den Kehrwert von 2/7, also 7/2, und multiplizieren die Zahl dann mit dem ersten Bruch also 3/4.

Brüche in Dezimalzahlen
Oft wird verlangt einen Bruch in eine Dezimalzahl umzuwandeln. Viele Schüler haben hierbei Schwierigkeiten, obwohl das Vorgehen immer gleich und somit einfach zu lernen ist. Um Bruchzahlen in Dezimalzahlen umzuwandeln muss man den Zähler mit dem Nenner dividieren und schon hast du das Ergebnis. Tipp: Wenn es sich um einen echten Bruch handelt muss das Ergebnis immer kleiner eins sein!
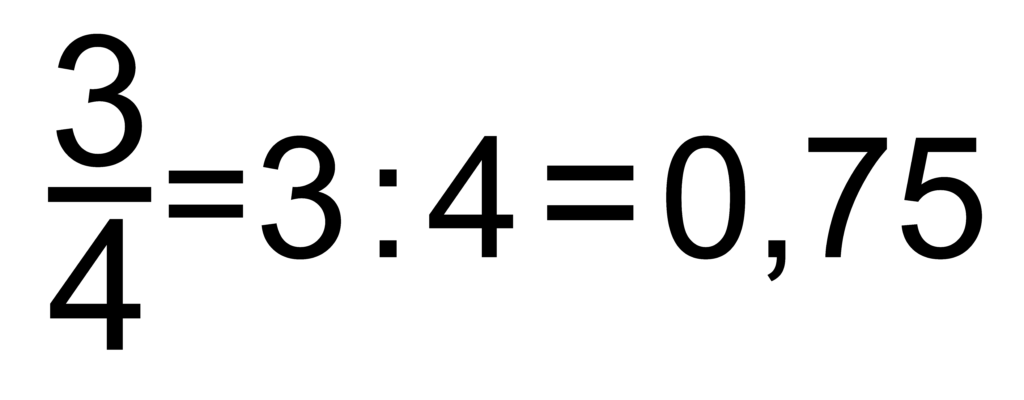
Du suchst Nachhilfe für dein Kind?
Bei GoStudent kannst du über unseren Link kostenlos einen Monat lang Nachhilfestunden im Wert von 125€ testen: https://mathemuffel.de/gostudent
🡳 Kostenlose Übungsblätter 🡳
Hier noch weiter gute Aufgabenblätter: https://www.uebungskoenig.de/mathe/6-klasse/brueche-bruchrechnen/
