Gleichungen 5.Klasse kostenlose Aufgabenblätter

Kostenlose Arbeitsblätter zum Download als PDF, zum Thema Gleichungen und Ungleichungen in der 5. Klasse. Viele Beispiele zum Üben!

Gleichung Definition

Einen mathematischen Ausdruck mit zwei Teilen, sogenannte Terme, welche mit einem Gleichheitszeichen(=) gleichgesetzt werden, werden Gleichungen genannt. Wir nennen die Terme „linke Seite“ und „rechte Seite“.

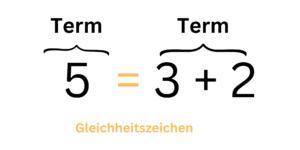
Wenn eine Gleichung ausschließlich aus zwei Zahlen besteht, können wir bestimmen ob diese eine wahre oder falsche Aussage ist.

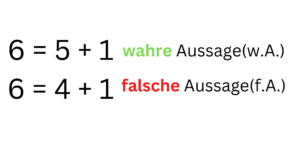
Die meisten Gleichungen beinhalten allerdings auch Variablen. Variablen sind Buchstaben, welche als Stellvertreter einer unbekannten Zahl dienen. Hier kann man nicht sofort sagen ob eine Aussage wahr ist oder nicht, da wir nicht alle Komponenten kennen. Wir können aber verschiedene Zahlen für die Variablen einsetzen und dann bestimmen ob dies eine wahre oder falsche Aussage ergibt.

Alle Zahlen, welche eingesetzt in die Gleichung, eine wahre Aussage ergeben, bilden die Lösungsmenge. Die Lösungsmenge wird mit einer geschwungenen Klammer angegeben und sollte es mehr als eine Lösung geben, trennt man diese mit einem Komma.

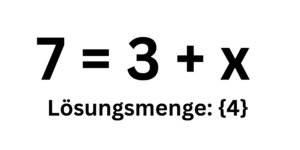
Neben vielen anderen Arten von Gleichungen, sind die vorerst am wichtigsten die linearen und die quadratischen Gleichungen. Lineare Gleichungen sind die einfachsten, beispielsweise 7 = 3 + x. Quadratische unterscheiden sich von den Linearen, weil sie x² enthalten, zum Beispiel x² = 16.

Gleichungen lösen

Kommen wir zum Lösen von Gleichungen. Dabei geht es darum, herauszufinden welche Zahl x sein muss damit wir eine wahre Aussage bekommen. Hier gibt es verschiedene Herangehensweisen:

1. Ausprobieren
2. Äquivalenzumformung

Wie der Name schon verrät, probierst du beim Ausprobieren einfach verschiedene Zahlen die du einsetzt und anschließend die Gleichung berechnest. Dies kann manchmal der einfache Weg sein und geht sehr schnell. Wenn es aber mehrere Lösungen gibt und etwas komplexer wird, dann sollte man zur Äquivalenzumformung greifen.

Äquivalenzumformung bedeutet, dass wir etwas verändern, sich aber der Wert der Gleichung nicht ändert. Damit die auch der Fall ist, müssen wir auf beiden Seiten die selben Zahlen addieren, subtrahieren, multiplizieren oder dividieren. Falls ihr eine Wiederholung zu den Grundrechenarten braucht, könnt ihr dies mit unserem Artikel zu Grundrechenarten machen!

Probieren wir das gleich mal mit 7 = 3 + x. Wir möchten, dass x allein auf der rechten Seite steht, also müssen wir das +3 wegbekommen. Hierfür subtrahieren wir 3, aber auf beiden Seiten, damit sich der Wert der Gleichung nicht ändert. An der rechten Seite notieren wir mit einem Äquivalenzstrich was genau wir machen möchten, in unserem Fall „-3“.

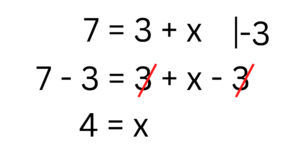
Anschließend berechnen wir beide Seiten. Links kommen wir auf 4, denn 7 – 3 = 4, und auf der rechten Seite heben sich +3 und -3 auf, denn 3 – 3= 0. Wir kommen zu dem Ergebnis 4 = x, dass bedeutet, unsere Lösungsmenge ist L = {4}.

Ungleichungen

Kommen wir zu Ungleichungen. Diese erkennt man daran, dass statt dem Gleichheitszeichen (=) eines der folgenden Ungleichheitszeichen: (<, ≤, >, ≥), zwischen der linken und der rechten Seite steht. Bei Ungleichungen sind also nicht beide Seiten gleich groß. (Zumindest nicht zwingend, bei ≤ und ≥ können sie gleich groß sein.

Lösen von Ungleichungen

Das Lösen von Ungleichungen funktioniert grundsätzlich gleich wie das der Gleichungen. Obwohl die Seiten nicht gleich groß sind, müssen wir bei der Äquivalenzumformung trotzdem weiterhin darauf achten, dass wir auf beiden Seiten das gleiche machen, um den Wert der Ungleichung nicht zu verändern. Zu beachten ist auch, dass die Lösungsmenge hier größer ausfallen kann. Starten wir einem Beispiel zu einer linearen Ungleichung: 7 > 3 + x

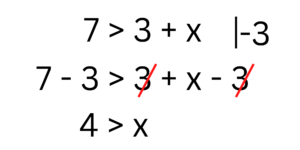
Der einzige Unterschied, ist also das Zeichen in der Mitte und die Lösungsmenge L = (-, 4), welche so viel bedeutet wie: von minus unendlich bis zur 3 sind alle Zahlen teil der Lösungsmenge. Die Klammern, mit welcher wir die Lösungsmenge einer Ungleichung angeben sind entweder ( oder [. Runde Klammern verwenden wir bei /- und bei Zahlen die nicht mehr inkludiert sind. In unserem Fall ist die 4 nicht mehr dabei, denn x ist kleiner als 4. Wäre die Ungleichung mit diesem Zeichen: ≥, dann wäre die Lösungsmenge L = (-,4]. Denn die eckige Klammer bedeutet, dass 4 dabei ist und auch die letzte Zahl ist welche dabei ist.

Inversion

Aber Achtung: es gibt bei den Ungleichungen eine wichtige Regel zu beachten! Diese Regel nennt sich Inversion, und besagt, dass wenn man die Ungleichung mit einer negativen Zahl multipliziert oder dividiert, dreht sich das Ungleichheitszeichen um. Schauen wir uns das gleich mal anhand eines Beispiels an: 6 > -3 · x.

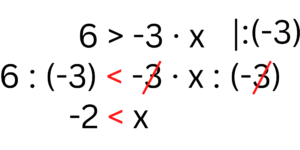
Tipp: Auf unserem YouTube Kanal gibt es eine ganze Playlist mit Videos zu Gleichungen und Ungleichungen!

🡳 Kostenlose Übungsblätter 🡳